부울대수와 카르노 맵
부울 대수
참과 거짓을 판별할 수 있는 논리적 명제를 수학적 표현의 논리 전개식으로 구현한 것
변수들의 진리표 관계를 대수식으로 표현하기 용이함
동일한 성능을 갖는 더 간단한 회로를 만들기에 편리함
부울 대수 기본 법칙 : 교환 법칙, 결합 법칙, 분배 법칙, 드모르간의 법칙
1 : 교환 법칙
순서를 바꿔도 성립한다.
1+0 = 0+1 = 1
1+1 = 1
1*1 = 1
나머지 연산의 경우는 다 0 (부울대수의 논리식은 대수학의 방식과 차이가 있다.)
AB는 둘 모두 참이면 참이라는 뜻이며, AND(교집합)와 같다.
A+B는 둘 중 하나만 참이면 참이라는 뜻이며 OR과 같다.

2 : 결합 법칙
괄호를 다르게 묶어도 성립

3 : 분배 법칙

4 : 드모르간의 법칙
A바(A')는 A의 부정(A의 여집합)과 같은 의미
A = 0일때 A' = 1
NOT과도 같은 의미. 참이면 거짓을, 거짓이면 참을 나타낸다.

부울 대수의 간소화
논리 회로식을 간소화하여 훃율성을 높이고 자원 낭비를 방지함
앞서 부울대수의 논리식은 대수학의 방식과 차이가 있음을 인지하자고 하였다.
1+0 = 0+1 = 1
1+1 = 1
1*1 = 1
나머지 연산의 경우는 다 0이다.
A + AB는 앞의 법칙에 따라 A(1+B) 로 나타낼 수 있다.
여기서 1+B는 B가 0이든 1이든 1이될 것이므로
A + AB = A가 된다.
같은 방식으로 AB + AB' = A(B+B') = A로 나타낼 수 있을 것이다.
그러나 이런 방법은 식이 복잡해지면 간소화하기가 쥰내 힘들어진다는 문제점이 있다.
카르노 맵(카노맵)
위와 같은 문제점을 해결하기 위해 고안된 방법이다.
예를들어 F = A’B’C’ + A’BC’ + AB’C’ + AB’C + ABC’ + ABC를 간소화 하는 문제가 있다고 가정하자.
1 : 우선 카르노 맵 표를 그린다.
이때 정해진 양식대로 그리는 것이 중요하다.
A, B, C가 1일때를 기준으로 00 01 11 10순으로 표를 구성한다.
(A, B, C가 1이면 A', B', C'는 당연히 0이 될 것이다.)

2 : F식의 각 항을 표의 행과 열의 곱으로 나타낼 수 있는 셀에 1을 적는다.
F의 첫번째 항인 A'B'C'는 A'행과 B'C'열의 곱으로 표현 가능하다.
이런 방법으로 각 셀에 1을 적어주면 다음과 같이 나타낼 수 있다.

3 : 1이 있는 부분끼리 직사각형 형태로 묶되, 그 숫자들의 합이 2의 n승이 되도록 한다.
직사각형 내의 1의 합이 2, 4, 6...형태가 되도록 묶는다. 여기서 검은색 숫자는 포함하지 않는다.

4 : 사각형 범위에 해당하는 열과 행에 속한 모든 값들 중 서로 부정관계가 되는 문자를 전부 제외시킨다.
이 문제의 경우 사각형 범위에 해당하는 행은 A, 열은 B'C' B'C BC BC'가 된다.
여기서 B와 B', C와 C'는 서로 부정관계이므로 전부 제외시킬 수 있다.

따라서 그림에서는 A만 남게 된다.
5 : 3번 4번 방법을 반복한다. 1의 합이 2의 n승 꼴이 될 수 있도록 직사각형으로 묶고 부정관계가 되는 문자들을 전부 제외시킨다.

이처럼 양끝에 사각형을 그릴 수 있는 경우는 양 끝이 서로 만난다고 생각하고 부정관계가 되는 문자를 전부 제외시켜야 한다.
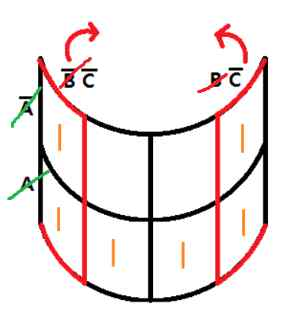
A', A행, B'C' BC'열이 범위에 해당하므로 부정관계가 되는 A', A와 B', B를 제외시키면 C'만 남게된다.
6 : 최종적으로 직사각형 내의 연산에서 나온 모든 결과값끼리 더해준다.
첫번째 사각형에서 A가, 두번째 사각형에서는 C'가 남게 되었으므로
최종적으로 F = A’B’C’ + A’BC’ + AB’C’ + AB’C + ABC’ + ABC를 간소화한 값은
A+C’가 된다.
예제) F = a'b + abc + bc 를 카노맵을 이용해 간편화하면?
1 : 우선 카노맵을 형식대로 그려본다.
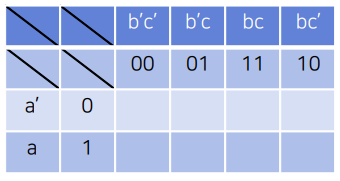
2 : F식의 각 항을 표의 행과 열의 곱으로 나타낼 수 있는 셀에 1을 적는다.
F = a'b + abc + bc에서 첫번째 항 a'b는 a'행과 bc열의 곱으로 나타낼 수 있는 것으로 본다.
그러나 두번째 항 abc는 a행과 bc열의 곱으로만 나타낼 수 있는 것으로 본다.

3 : 1이 있는 부분끼리 직사각형 형태로 묶되, 그 숫자들의 합이 2의 n승이 되도록 한다.

4 : 사각형 범위에 해당하는 열과 행에 속한 모든 값들 중 서로 부정관계가 되는 문자를 전부 제외시킨다.
해당 범위에서는 a'과 a만 제외시킬 수 있으므로 bc값이 남게된다.
5 : 3, 4번 방법을 반복한다.

묶을 수 있는 모든 방법으로 묶고, 부정관계끼리 제외시키는 것을 반복한다.
그림에서는 c와 c'을 제외시킬 수 있으므로 a'b가 남게된다.
6 : 사각형에서 나온 값을 전부 더한다.
따라서 F = a'b + abc + bc를 카노맵으로 간소화한 값은 bc + a'b가 된다.
지금까지는 카노맵이 삼변수인 경우를 가지고 알아보았지만 사변수, 오변수의 경우에서도 같은 방법을 이용할 수 있다고 한다. 그러나 묶는 방법이 많아지고, 어떻게 묶는냐에 따라 답이 달라질 수 있으니 주의하자. 자세히 알고 싶은 분들은 이곳을 참고하면 좋겠다.
'CS 공부 > 컴퓨터 구조' 카테고리의 다른 글
| 컴퓨터 구조 06 : CPU 구성요소/동작, 레지스터 종류, 명령어 사이클 (0) | 2022.01.21 |
|---|---|
| 컴퓨터 구조 05 : 조합 논리 회로, 순서 논리 회로 (0) | 2022.01.20 |
| 컴퓨터 구조 03 : 실수표현법, 논리게이트 (0) | 2022.01.19 |
| 컴퓨터 구조 02 : 진법 변환, 부호비트 방식, 보수법, Pack/Unpack 연산 (0) | 2022.01.19 |
| 컴퓨터 구조 01 : 컴퓨터 구성요소와 데이터의 표현 (0) | 2022.01.19 |

